内容

• 脚步
• 第 1 部分（共 2 部分）：基础知识
• 第 2 部分（共 2 部分）：扩展矩阵变换以解决 SLAE
• 提示

方程组是一组两个或多个方程，这些方程具有一组共同的未知数，因此具有共同的解。线性方程组的图形是两条直线，系统的解是这两条直线的交点。要求解此类线性方程组，使用矩阵非常有用且方便。

脚步

第 1 部分（共 2 部分）：基础知识

1. 1 术语。 线性方程组由各种组件组成。变量由字母字符（通常是 x 或 y）表示，表示您尚不知道且需要查找的数字。常量是不改变其值的特定数字。系数就是变量前面的数字，也就是变量乘以的数字。
   • 例如，对于线性方程，2x + 4y = 8，x 和 y 是变量，8 是常数，数字 2 和 4 是系数。
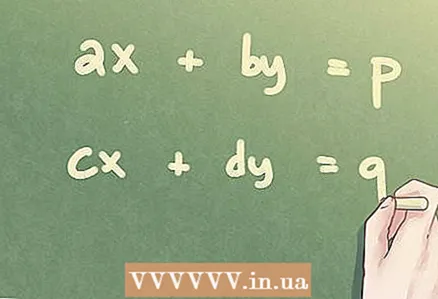2. 2 线性方程组的形式。 具有两个变量的线性代数方程 (SLAE) 系统可以写成如下：ax + by = p，cx + dy = q。任何常数 (p, q) 都可以为零，但每个方程必须至少包含一个变量 (x, y)。
3. 3 矩阵表达式。 任何 SLAE 都可以写成矩阵形式，然后使用矩阵的代数性质来求解。以矩阵形式写方程组时，A代表矩阵的系数，C代表常数矩阵，X代表未知矩阵。
   • 例如，上面的 SLAE 可以改写为以下矩阵形式：A x X = C。
4. 4 扩展矩阵。 扩展矩阵是通过将自由项（常数）矩阵向左移而得到的。如果您有两个矩阵 A 和 C，则扩展后的矩阵将如下所示：
   • 例如，对于以下线性方程组：
     2x + 4y = 8
     x + y = 2
     展开后的矩阵将是 2x3，如下所示：

第 2 部分（共 2 部分）：扩展矩阵变换以解决 SLAE

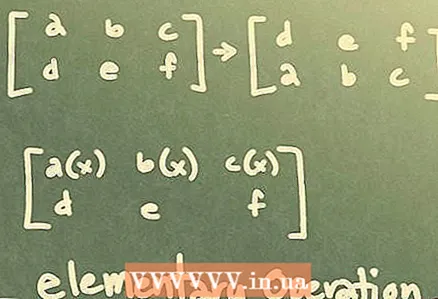1. 1 基本操作。 您可以对矩阵执行某些操作，从而获得与原始矩阵等效的矩阵。此类操作称为基本操作。例如，要求解一个 2x3 矩阵，您需要执行行运算以将矩阵变为三角形形式。此类操作可以是：
   • 两行的排列。
   • 将一个字符串乘以一个非零数。
   • 将一个字符串相乘并将其添加到另一个字符串。
2. 2 第二行乘以一个非零数。 如果您希望第二行为零，则可以将该行乘以使其成为可能。
   • 例如，如果您有一个这样的矩阵：
     
     
     您可以保留第一行并使用它在第二行获得零。为此，您必须首先将第二行乘以 2：
3. 3 再乘。 要获得第一行的零，您可能需要使用类似的操作再次相乘。
   • 在上面的示例中，您需要将第二行乘以 -1：
     
     
     乘法后，矩阵将如下所示：
4. 4 将第一行添加到第二行。 添加行以获得零代替第一列和第二行。
   • 在我们的示例中，添加两行以获得以下结果：
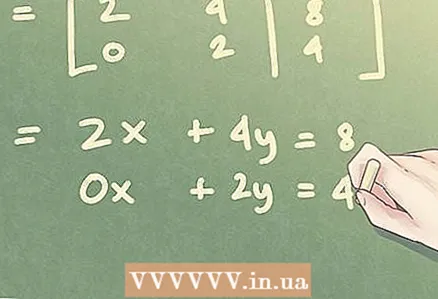5. 5 为三角矩阵写一个新的线性方程组。 一旦你得到了三角矩阵，你就可以回到 SLAE。矩阵的第一列对应未知变量 x，第二列对应未知变量 y。第三列对应于方程的截距。
   • 对于我们的示例，新的线性方程组将采用以下形式：
6. 6 求解其中一个变量的方程。 在新的 SLAE 中，确定哪个变量最容易找到并求解方程。
   • 在我们的例子中，从末端求解更方便，即从最后一个方程到第一个方程，从下到上。从第二个方程，我们可以很容易地找到 y 的解，因为我们去掉了 x，所以 y = 2。
7. 7 用替换法求第二个未知数。 找到其中一个变量后，您可以将其代入第二个方程以找到第二个变量。
   • 在我们的示例中，只需将第一个方程中的 y 替换为 2 即可找到未知的 x：

提示

• 矩阵元素通常称为标量。
• 要求解 2x3 矩阵，您必须执行基本行运算。您不能对列执行这些操作。