内容

• 脚步
• 提示

有理函数的形式为 y = N (x) / D (x)，其中 N 和 D 是多项式。要准确地绘制这样的函数，您需要具备良好的代数知识，包括微分计算。考虑以下示例： 是 = (2X - 6X + 5)/(4X + 2).

脚步

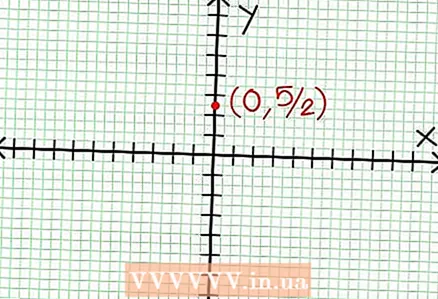1. 1 找到图形的 y 轴截距。 为此，将 x = 0 代入函数并得到 y = 5/2。因此，图形与 Y 轴的交点具有坐标 (0, 5/2)。将此点放置在坐标平面上。
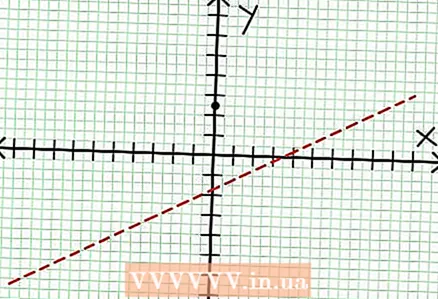2. 2 找到水平渐近线。 将分子除以分母（在列中）以确定“y”的行为，其中“x”的值趋于无穷大。在我们的例子中，除法将是 是 = (1/2)X - (7/4) + 17/(8X + 4）。对于“x”的大正值或负值 17 / (8X + 4) 趋于零，图形接近函数给出的直线 是 = (1/2)X - (7/4).使用虚线绘制此函数。
   • 如果分子的次数小于分母的次数，则不能将分子除以分母，渐近线将由函数描述 在 = 0.
   • 如果分子的次数等于分母的次数，则渐近线是一条水平线，等于“x”处最高次数的系数之比。
   • 如果分子的次数比分母的次数多1，则渐近线是一条倾斜的直线，其斜率等于“x”处的系数与最高次数的比值。
   • 如果分子的度数比分母的度数大2、3等，那么对于大数值国民服役|意义 在 以平方、三次或其他多项式的形式趋于无穷大（正或负）。在这种情况下，您很可能不需要构建分子除以分母得到的函数的精确图。
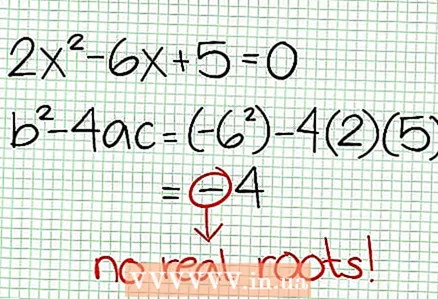3. 3 找到函数的零点。 有理函数在其分子为零时有零点，即 N (国民服役) = 0。在我们的例子中，2X - 6X + 5 = 0. 这个二次方程的判别式： 乙 - 4交流电 = 6 - 4 * 2 * 5 = 36 - 40 = -4。由于判别式为负，则 N (国民服役)，因此 F (国民服役) 没有真正的根。有理函数的图形不与X轴相交。如果函数有零（根），则将它们放在坐标平面上。
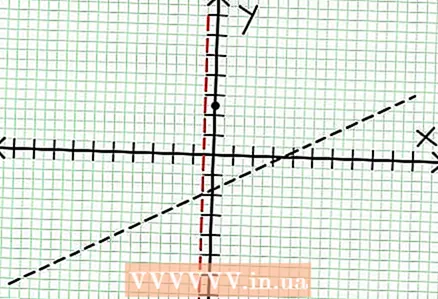4. 4 求垂直渐近线。 为此，请将分母设置为零。在我们的例子中，4X + 2 = 0 和 国民服役 = -1/2。使用虚线绘制垂直渐近线。如果为了某种价值 国民服役 N (国民服役) = 0 和 D (国民服役) = 0，则垂直渐近线要么存在要么不存在（这种情况很少见，但最好记住它）。
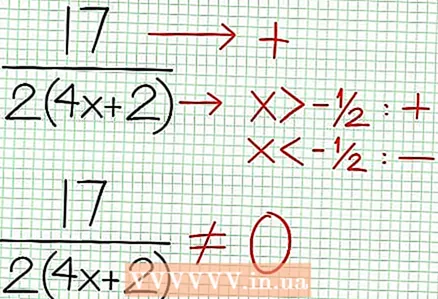5. 5 查看分子除以分母的余数。 它是正数、负数还是零？在我们的示例中，余数是 17，这是正数。分母 4X + 2 垂直渐近线右侧为正，左侧为负。这意味着大正值的有理函数图 国民服役 从上面接近渐近线，对于大的负值 国民服役 - 从下面。自 17 / (8X + 4) 永远不等于零，则此函数的图形永远不会与函数指定的直线相交 在 = (1/2)国民服役 - (7/4).
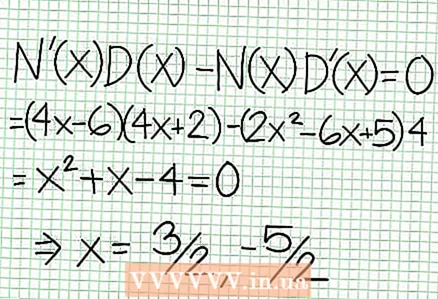6. 6 寻找局部极值。 N '(X) D (X) - N (X) D’(X) = 0。在我们的例子中，N’(X) = 4X - 6 和 D'(X) = 4.N’(X) D (X) - N (X) D’(X) = (4X - 6)(4X + 2) - (2X - 6X + 5)*4 = X + X - 4 = 0. 解这个方程，你会发现 X = 3/2 和 X = -5/2。 （这些不是完全准确的值，但它们适用于不需要超精度的情况。）
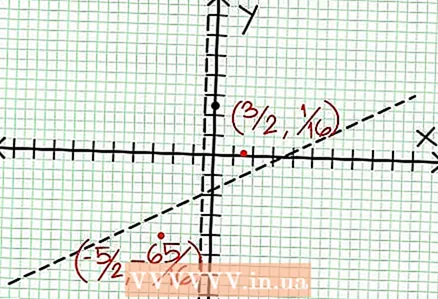7. 7 找到价值 在 对于每个局部极值。 为此，请替换值 国民服役 为原有理函数。在我们的示例中，f (3/2) = 1/16 和 f (-5/2) = -65/16。在坐标平面上留出点 (3/2, 1/16) 和 (-5/2, -65/16)。由于计算基于近似值（来自上一步），因此找到的最小值和最大值也不完全准确（但可能非常接近精确值）。 （点 (3/2, 1/16) 非常接近局部最小值。从第 3 步开始，我们知道 在 总是积极的 国民服役> -1/2，我们发现了一个很小的值（1/16）；因此，这种情况下的误差值非常小。）
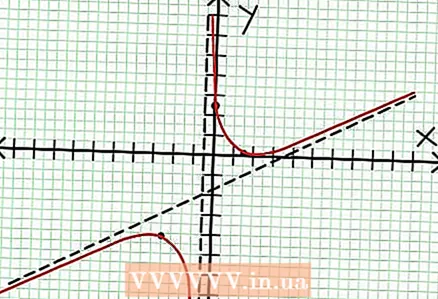8. 8 连接待定点并将图形平滑地扩展到渐近线（不要忘记图形接近渐近线的正确方向）。 请记住，图形不得与 X 轴交叉（参见步骤 3）。该图也不与水平和垂直渐近线相交（参见步骤 5）。除了在上一步中找到的极值点之外，不要改变图表的方向。

提示

• 如果您严格按顺序执行上述步骤，则无需计算二阶导数（或类似的复数）来测试您的解决方案。
• 如果不需要计算量的值，可以通过计算一些额外的坐标对来代替寻找局部极值（国民服役, 在) 在每对渐近线之间。此外，如果您不关心所描述的方法是如何工作的，那么请不要惊讶为什么您找不到导数并求解方程 N'(X) D (X) - N (X) D’(X) = 0.
• 在某些情况下，您将不得不使用高阶多项式。如果您无法使用因式分解、公式等找到精确解，则使用数值方法（例如牛顿法）估计可能的解。
• 在极少数情况下，分子和分母共享一个公共变量因子。根据所描述的步骤，这将导致零和同一位置的垂直渐近线。但是，这是不可能的，解释是以下之一：
  • N 中的零 (国民服役) 在 D (国民服役）。图 F (国民服役) 在这一点上趋于零，但没有在那里定义。通过在该点周围画一个圆圈来表明这一点。
  • N 中的零 (国民服役) 和 D 中的零 (国民服役) 具有相同的多重性。该图在此值处接近某个非零点 国民服役但未在其中定义。通过在该点周围画一个圆圈来表明这一点。
  • N 中的零 (国民服役) 在 D (国民服役）。这里有一条垂直渐近线。