作者:
Virginia Floyd
创建日期:
11 八月 2021
更新日期:
1 七月 2024

内容
如果你知道如何将两个矩阵相乘,你就可以开始“划分”矩阵了。 “除法”一词用引号括起来,因为矩阵实际上不能被除法。除法运算被一个矩阵乘以第二个矩阵的逆矩阵的运算代替。为简单起见,考虑一个整数示例:10 ÷ 5。求 5 的倒数:5 或 /5,然后用乘法代替除法:10 x 5;除法和乘法的结果是一样的。因此,认为可以用逆矩阵乘法代替除法。通常,此类计算用于求解线性方程组。
简要总结
- 你不能划分矩阵。不是除法,而是将一个矩阵乘以第二个矩阵的逆矩阵。两个矩阵的“除法” [A] ÷ [B] 的写法如下:[A] * [B] 或 [B] * [A]。
- 如果矩阵 [B] 不是方阵,或者它的行列式是 0,写下“没有明确的解”。否则,找到矩阵 [B] 的行列式并转到下一步。
- 求逆:[B]。
- 将矩阵相乘以找到 [A] * [B] 或 [B] * [A]。请记住,矩阵相乘的顺序会影响最终结果(即,结果可能会有所不同)。
脚步
第 1 部分(共 3 部分):测试矩阵的可分性
 1 理解矩阵的“除法”。 事实上,矩阵不能被划分。没有像“将一个矩阵除以另一个”这样的数学运算。除法被替换为将一个矩阵乘以第二个矩阵的逆矩阵。即记法[A]÷[B]不正确,所以用如下记法代替:[A]*[B]。由于两个条目在标量值的情况下是等效的,理论上我们可以谈论矩阵的“除法”,但使用正确的术语仍然更好。
1 理解矩阵的“除法”。 事实上,矩阵不能被划分。没有像“将一个矩阵除以另一个”这样的数学运算。除法被替换为将一个矩阵乘以第二个矩阵的逆矩阵。即记法[A]÷[B]不正确,所以用如下记法代替:[A]*[B]。由于两个条目在标量值的情况下是等效的,理论上我们可以谈论矩阵的“除法”,但使用正确的术语仍然更好。 - 注意 [A] * [B] 和 [B] * [A] 是不同的操作。可能需要执行这两种操作才能找到所有可能的解决方案。
- 例如,代替
写下来
.
你可能需要计算得到不同的结果。
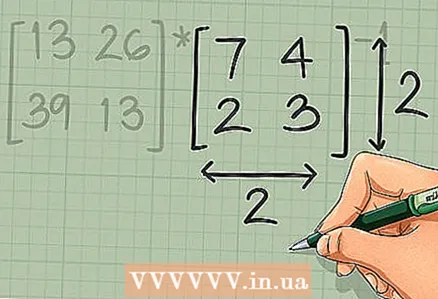 2 确保您“除”另一个矩阵的矩阵是正方形。 要求矩阵的求逆(求矩阵的逆),它必须是方阵,即具有相同的行数和列数。如果逆矩阵不逆,则无定解。
2 确保您“除”另一个矩阵的矩阵是正方形。 要求矩阵的求逆(求矩阵的逆),它必须是方阵,即具有相同的行数和列数。如果逆矩阵不逆,则无定解。 - 同样,矩阵在这里不可“整除”。在操作 [A] * [B] 中,所描述的条件是指矩阵 [B]。在我们的例子中,这个条件指的是矩阵
- 可以反转的矩阵称为非退化矩阵或正则矩阵。不能求逆的矩阵称为退化矩阵或奇异矩阵。
- 同样,矩阵在这里不可“整除”。在操作 [A] * [B] 中,所描述的条件是指矩阵 [B]。在我们的例子中,这个条件指的是矩阵
 3 检查两个矩阵是否可以相乘。 要将两个矩阵相乘,第一个矩阵中的列数必须等于第二个矩阵中的行数。如果条目[A]*[B]或[B]*[A]中不满足此条件,则无解。
3 检查两个矩阵是否可以相乘。 要将两个矩阵相乘,第一个矩阵中的列数必须等于第二个矩阵中的行数。如果条目[A]*[B]或[B]*[A]中不满足此条件,则无解。 - 例如,如果矩阵 [A] 的大小为 4 x 3,矩阵 [B] 的大小为 2 x 2,则无解。你不能乘 [A] * [B] 因为 4 ≠ 2,你不能乘 [B] * [A] 因为 2 ≠ 3。
- 请注意,逆矩阵 [B] 始终具有与原始矩阵 [B] 相同的行数和列数。不需要找到逆矩阵来检查两个矩阵是否可以相乘。
- 在我们的示例中,两个矩阵的大小都是 2 x 2,因此它们可以按任意顺序相乘。
 4 找到 2 × 2 矩阵的行列式。 请记住:只有当矩阵的行列式不为零时,您才能反转矩阵(否则,您无法反转矩阵)。以下是如何找到 2 x 2 矩阵的行列式:
4 找到 2 × 2 矩阵的行列式。 请记住:只有当矩阵的行列式不为零时,您才能反转矩阵(否则,您无法反转矩阵)。以下是如何找到 2 x 2 矩阵的行列式: - 2 x 2 矩阵: 矩阵的行列式
等于 ad - bc。即从主对角线(经过左上角和右下角)的元素的乘积中,减去另一对角线(经过右上角和左下角)的元素的乘积。
- 例如,矩阵的行列式
等于 (7) (3) - (4) (2) = 21 - 8 = 13。行列式非零,所以这个矩阵可以反转。
- 2 x 2 矩阵: 矩阵的行列式
 5 找到较大矩阵的行列式。 如果矩阵的大小为 3 x 3 或更大,则行列式计算稍微困难一些。
5 找到较大矩阵的行列式。 如果矩阵的大小为 3 x 3 或更大,则行列式计算稍微困难一些。 - 3 x 3 矩阵:选择任何项目并划掉它所在的行和列。求所得2×2矩阵的行列式,然后乘以所选元素;在特殊表中指定行列式的符号。对与您选择的项目位于同一行或列中的其他两个项目重复此过程。然后找到接收到的(三个)行列式的总和。阅读本文以了解有关如何找到 3 x 3 矩阵的行列式的更多信息。
- 大矩阵:最好使用图形计算器或软件来寻找此类矩阵的行列式。该方法与求3×3矩阵行列式的方法类似,但手动应用比较繁琐。例如,要找到 4 x 4 矩阵的行列式,您需要找到四个 3 x 3 矩阵的行列式。
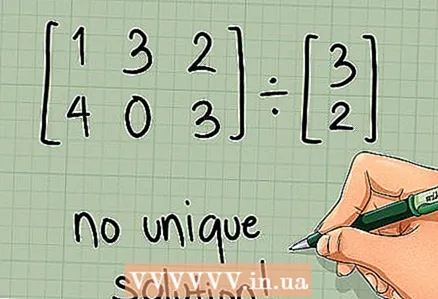 6 继续计算。 如果矩阵不是方阵或其行列式为零,则写“无明确解”,即计算过程完成。如果矩阵是方阵并且有一个非零行列式,跳到下一节。
6 继续计算。 如果矩阵不是方阵或其行列式为零,则写“无明确解”,即计算过程完成。如果矩阵是方阵并且有一个非零行列式,跳到下一节。
第 2 部分(共 3 部分):求逆矩阵
 1 交换 2 x 2 矩阵的主对角线的元素。 给定一个 2 × 2 矩阵,使用快速逆方法。首先,交换左上角元素和右下角元素。例如:
1 交换 2 x 2 矩阵的主对角线的元素。 给定一个 2 × 2 矩阵,使用快速逆方法。首先,交换左上角元素和右下角元素。例如: →
- 笔记: 大多数人使用计算器来反转 3 x 3(或更大)的矩阵。如果您需要手动执行此操作,请转到本节末尾。
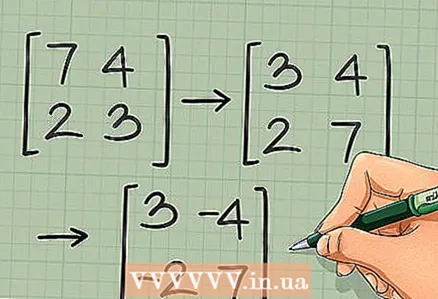 2 不要交换剩下的两个元素,而是改变它们的符号。 也就是说,将右上角的元素和左下角的元素乘以 -1:
2 不要交换剩下的两个元素,而是改变它们的符号。 也就是说,将右上角的元素和左下角的元素乘以 -1: →
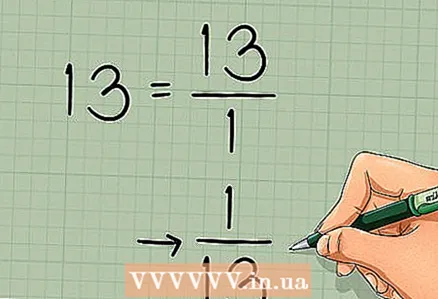 3 求行列式的倒数。 这个矩阵的行列式在上一节中已经找到,所以我们不再计算它。行列式的逆写成如下:1/(行列式):
3 求行列式的倒数。 这个矩阵的行列式在上一节中已经找到,所以我们不再计算它。行列式的逆写成如下:1/(行列式): - 在我们的例子中,行列式是 13。反转值:
.
- 在我们的例子中,行列式是 13。反转值:
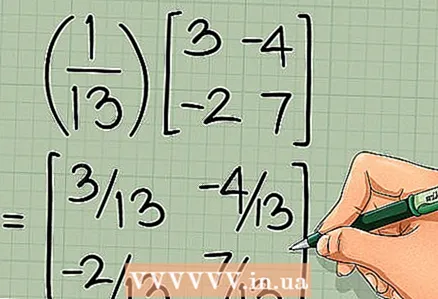 4 将结果矩阵乘以行列式的倒数。 将新矩阵的每个元素乘以行列式的逆。最终矩阵将是原始 2 x 2 矩阵的逆矩阵:
4 将结果矩阵乘以行列式的倒数。 将新矩阵的每个元素乘以行列式的逆。最终矩阵将是原始 2 x 2 矩阵的逆矩阵:
=
 5 检查计算是否正确。 为此,请将原始矩阵乘以其逆矩阵。如果计算正确,原始矩阵与逆矩阵的乘积将给出单位矩阵:
5 检查计算是否正确。 为此,请将原始矩阵乘以其逆矩阵。如果计算正确,原始矩阵与逆矩阵的乘积将给出单位矩阵: ...如果测试成功,请继续下一部分。
- 在我们的例子中:
.
- 有关如何乘以矩阵的更多信息,请阅读本文。
- 注意:矩阵乘法的运算不是可交换的,即矩阵的顺序很重要。但是当原始矩阵乘以其逆矩阵时,任何阶都会导致单位矩阵。
- 在我们的例子中:
 6 求 3 x 3 矩阵的逆矩阵 (或更大)。 如果您已经熟悉这个过程,最好使用图形计算器或专用软件。如果需要手动求逆矩阵,过程简述如下:
6 求 3 x 3 矩阵的逆矩阵 (或更大)。 如果您已经熟悉这个过程,最好使用图形计算器或专用软件。如果需要手动求逆矩阵,过程简述如下: - 在原始矩阵的右侧加入单位矩阵 I。例如,[B] → [B |一世]。对于单位矩阵,主对角线的所有元素都等于1,其他所有元素都等于0。
- 简化矩阵,使其左侧变为阶梯状;继续简化,使左侧成为单位矩阵。
- 简化后,矩阵将采用以下形式:[I |乙]。也就是说,它的右边是原始矩阵的逆矩阵。
第 3 部分(共 3 部分):矩阵乘法
 1 写出两种可能的表达方式。 两个标量相乘的运算是可交换的,即 2 x 6 = 6 x 2。在矩阵乘法的情况下不是这种情况,因此您可能需要解决两个表达式:
1 写出两种可能的表达方式。 两个标量相乘的运算是可交换的,即 2 x 6 = 6 x 2。在矩阵乘法的情况下不是这种情况,因此您可能需要解决两个表达式: - X = [A] * [B] 是方程的解 X[B] = [A]。
- X = [B] * [A] 是方程 [B] 的解X = [A]。
- 在等式两边执行每个数学运算。如果 [A] = [C] 那么 [B] [A] ≠ [C] [B] 因为 [B] 在 [A] 的左边但在 [C] 的右边。
 2 确定最终矩阵的大小。 最终矩阵的大小取决于相乘矩阵的大小。最终矩阵的行数等于第一个矩阵的行数,最终矩阵的列数等于第二个矩阵的列数。
2 确定最终矩阵的大小。 最终矩阵的大小取决于相乘矩阵的大小。最终矩阵的行数等于第一个矩阵的行数,最终矩阵的列数等于第二个矩阵的列数。 - 在我们的例子中,两个矩阵的大小
和
是 2 x 2,所以原始矩阵的大小将为 2 x 2。
- 考虑一个更复杂的例子:如果矩阵 [A] 的大小是 4 x 3,矩阵 [B] 的大小为 3 x 3,那么最终矩阵 [A] * [B] 将是 4 x 3。
- 在我们的例子中,两个矩阵的大小
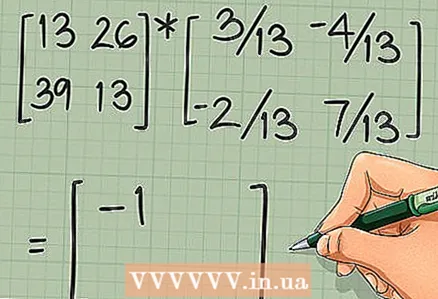 3 找出第一个元素的值。 阅读本文或记住以下基本步骤:
3 找出第一个元素的值。 阅读本文或记住以下基本步骤: - 要找到最终矩阵 [A] [B] 的第一个元素(第一行,第一列),计算矩阵 [A] 第一行的元素与矩阵 [B] 第一列的元素的点积]。在 2 x 2 矩阵的情况下,点积计算如下:
.
- 在我们的例子中:
...因此,最终矩阵的第一个元素将是以下元素:
- 要找到最终矩阵 [A] [B] 的第一个元素(第一行,第一列),计算矩阵 [A] 第一行的元素与矩阵 [B] 第一列的元素的点积]。在 2 x 2 矩阵的情况下,点积计算如下:
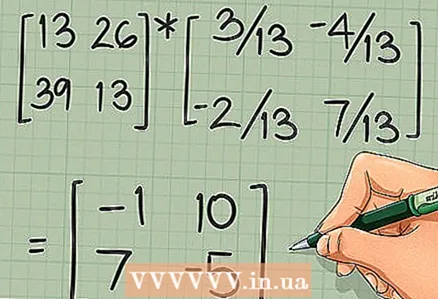 4 继续计算点积以找到最终矩阵的每个元素。 例如,位于第二行第一列的元素等于矩阵[A]的第二行和矩阵[B]的第一列的点积。尝试自己找到剩余的项目。您应该得到以下结果:
4 继续计算点积以找到最终矩阵的每个元素。 例如,位于第二行第一列的元素等于矩阵[A]的第二行和矩阵[B]的第一列的点积。尝试自己找到剩余的项目。您应该得到以下结果: - 如果您需要寻找其他解决方案:
提示
- 矩阵可以分为标量;为此,矩阵的每个元素都除以一个标量。
- 例如,如果矩阵
除以2,你得到矩阵
- 例如,如果矩阵
警告
- 当涉及矩阵计算时,计算器并不总是给出绝对准确的结果。例如,如果计算器声称该项目是一个非常小的数字(例如 2E),则该值很可能为零。
附加文章
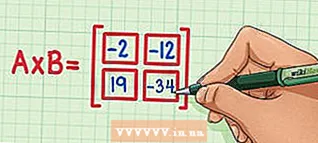 如何乘以矩阵
如何乘以矩阵  如何找到 3x3 矩阵的逆矩阵
如何找到 3x3 矩阵的逆矩阵  如何找到 3X3 矩阵的行列式
如何找到 3X3 矩阵的行列式  如何找到二次函数的最大值或最小值
如何找到二次函数的最大值或最小值  如何计算频率
如何计算频率  如何解二次方程
如何解二次方程  如何在没有卷尺的情况下测量高度
如何在没有卷尺的情况下测量高度  如何手动找到数字的平方根
如何手动找到数字的平方根  如何将毫升转换为克
如何将毫升转换为克  如何将二进制转换为十进制
如何将二进制转换为十进制  如何计算pi值
如何计算pi值  如何将十进制转换为二进制
如何将十进制转换为二进制  如何计算概率
如何计算概率  如何将分钟转换为小时
如何将分钟转换为小时



