内容

• 踩
• 方法1之3：第一个简单的任务
• 方法2之3：计算特定结果的期望值
• 方法3之3：了解概念
• 尖端
• 生活必需品

期望值是一个统计术语，是一个概念，用于确定某项操作的有用性或有害性。要计算期望值，必须对特定情况下的每个结果以及相关的概率或特定结果将发生的概率有一个很好的了解。下面的步骤提供了一些示例练习，以帮助您理解期望值的概念。

踩

方法1之3：第一个简单的任务

1. 阅读声明。 在开始考虑所有可能的结果和可能性之前，了解此问题很重要。例如，一个骰子游戏每场收费10欧元。一个六角形骰子滚动一次，您的赢取额取决于您滚动的次数。如果投出6，则赢得30欧元； 5人赚20欧元；其他任何数字都不会产生任何结果。
2. 列出所有可能的结果。 它有助于列出给定情况下的所有可能结果。在上面的示例中，有6种可能的结果。它们是：（1）投出1并输掉10美元，（2）投出2并输掉10美元，（3）投出3并输掉10美元，（4）投出4并输掉10美元，（5）投出5并赢得$ 10，（6）投出6并赢得$ 20。
   • 请注意，每个结果比上述金额少10欧元，因为无论结果如何，您都必须先为每场比赛支付10欧元。
3. 确定每个结果的可能性。 在这种情况下，任何6个结果的概率都是相同的。随机数被滚动的概率是1 /6。为了更容易记下来，我们将使用计算器将分数（1/6）写成小数：0.167。将此概率写在每个结果的旁边，特别是如果您要解决每个结果具有不同概率的问题时，尤其如此。
   • 您的1/6计算器可能会产生类似0.166667的值。我们将此值舍入为0.167，以便在不牺牲精度的情况下更轻松地进行计算。
   • 如果要获得非常准确的结果，请不要将其设置为小数，只需在公式中输入1/6并在计算器上进行计算即可。
4. 记录每个结果的值。 将结果的$乘以结果出现的概率，以计算该结果将为期望值贡献多少钱。例如，滚动1的结果为-$ 10，滚动1的概率为0.167。因此，抛出1的值是（-10） *（0.167）。
   • 如果您拥有可以同时执行多项操作的计算器，则现在无需计算这些结果。如果输入整个方程，将得到更准确的结果。
5. 将每个结果的值相加以获得事件的预期值。 继续上面的示例，骰子游戏的期望值为：（-10 * 0.167）+（-10 * 0.167）+（-10 * 0.167）+（-10 * 0.167）+（10 * 0.167）+（20 * 0.167），或-€1.67。因此，您可以期望每次游戏（每次游戏）每次亏损1.67美元。
6. 计算期望值的含义是什么。 在上面的示例中，我们确定预期的利润（亏损）为-每掷1.67欧元。 1场比赛这是不可能的结果；您可能会损失10欧元，赢得10欧元或赢得20欧元。但是从长远来看，期望值是有用的平均概率。如果继续玩这个游戏，平均每场游戏您将损失约1.67美元。考虑期望值的另一种方法是为游戏分配一定的成本（或收益）。您应该只玩这个游戏，如果您发现它值得，请尽情享受它，每次花费1.67美元。
   • 情况重复的次数越多，期望值就越能准确地表示实际的平均结果。例如，也许您连续玩了5次游戏，每次都输了，导致平均损失$ 10。但是，如果您再玩1000次游戏，则平均结果将越来越接近预期值-每场游戏€1.67。该原理称为“大数定律”。

方法2之3：计算特定结果的期望值

1. 使用此方法可以计算出发生特定图案之前需要翻转的平均硬币数量。 例如，您可以使用该方法找出要翻转的硬币的预期数量，直到连续两次出现正面为止。这个问题比关于期望值的标准问题要棘手，因此，如果您不熟悉期望值的概念，请先阅读本文的以上部分。
2. 假设我们正在寻找值x。 您正在尝试确定平均需要翻转多少枚硬币才能连续获得两个头。现在，我们进行比较以找到答案。我们称呼我们正在寻找x的答案。我们逐步进行必要的比较。目前，我们有以下内容：
   • x = ___
3. 想想如果第一次翻转产生硬币会发生什么。 在一半的情况下就是这种情况。在这种情况下，您已经“浪费”了翻滚，而连续两次摇头的机会没有改变。与掷硬币一样，预计您必须连续掷两次平均头才能掷出平均次数。换句话说，您将希望滚动x次，再加上您已经玩过的次数。以等式的形式：
   • x =（0.5）（x +1）+ ___
   • 我们将继续考虑其他情况，以填补空白。
   • 如果更简单或必要，则可以使用分数而不是小数。
4. 想想当你扔头时会发生什么。 第一次丢杯的机率是0.5（或1/2）。这似乎更接近于连续两次扔头的目标，但是多少呢？最简单的查找方法是在第二卷上考虑您的选择：
   • 如果第二次掷硬币，我们又回到了起点。
   • 如果第二次也是杯赛，那么我们就完成了！
5. 了解如何计算两个事件都将发生的概率。 现在我们知道您有50％的机会将杯子扔掉，但是您连续两次将杯子扔掉的机会是多少？要计算此概率，请将两者的概率相乘。在这种情况下，它是0.5 x 0.5 = 0.25。当然，这也是您先滚动头再滚动尾巴的机会，因为它们都有0.5的机会发生：0.5 x 0.5 = 0.25。
6. 将“先头后尾”的结果添加到等式中。 现在我们已经计算出发生此事件的可能性，我们可以继续扩展方程式。我们有0.25（或1/4）的机会浪费掉两次掷球而没有前进。但是现在我们仍然需要平均增加x倍的数量才能获得想要获得的结果，再加上我们已经抛出的2个。以等式形式，它变为（0.25）（x + 2），我们现在可以将其添加到等式中：
   • x =（0.5）（x +1）+（0.25）（x + 2）+ ___
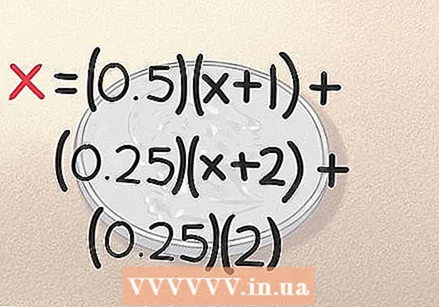7. 将“标题，标题”的结果添加到等式中。 如果朝头掷硬币，头两个抛硬币就完成了。您仅在2次掷球中就得到了结果。正如我们前面提到的，发生这种情况的可能性为0.25，因此，此等式为（0.25）（2）。我们的比较现已完成：
   • x =（0.5）（x +1）+（0.25）（x + 2）+（0.25）（2）
   • 如果您不确定是否已经考虑了所有可能的情况，则有一种简便的方法来检查方程是否完整。等式各部分中的第一个数字表示事件发生的概率。这总等于1。在这里，0.5 + 0.25 + 0.25 = 1，所以我们知道我们已经包括了每种情况。
8. 简化方程式。 让我们通过乘法使方程式变得容易一些。请记住，如果您在括号中看到以下内容：（0.5）（x + 1），则将0.5乘以第二组括号中的每个项。这将为您提供以下内容：0.5x +（0.5）（1）或0.5x + 0.5。让我们为方程式中的每个术语执行此操作，然后合并这些术语，使它们看起来都更加简单：
   • x = 0.5x +（0.5）（1）+ 0.25x +（0.25）（2）+（0.25）（2）
   • x = 0.5x + 0.5 + 0.25x + 0.5 + 0.5
   • x = 0.75x + 1.5
9. 解决x。 如同在任何方程式中一样，您将需要在方程式的一侧隔离x以进行计算。请记住，x表示“连续两次要掷出硬币所需投入的平均硬币数”。当我们计算出x时，我们也找到了答案。
   • x = 0.75x + 1.5
   • x-0.75x = 0.75x + 1.5-0.75x
   • 0.25倍= 1.5
   • （0.25x）/（0.25）=（1.5）/（0.25）
   • x = 6
   • 平均而言，在掷头两次之前，您将不得不抛掷硬币6次。

方法3之3：了解概念

1. 实际期望值是多少。 期望值不一定是最明显或合乎逻辑的结果。有时，期望值在给定情况下甚至可能是不可能的值。例如，对于奖金不超过10欧元的游戏，期望值可以为+ 5欧元。期望值指示的是特定事件的价值。如果游戏的期望价值为+€5，那么您可以玩游戏，如果您认为值得每场比赛花费时间和金钱。如果另一个游戏的期望值为-$ 20，则只有在您认为每个游戏都值$ 20的情况下，您才玩它。
2. 了解独立事件的概念。 在日常生活中，我们许多人认为当一些好事发生时，我们会有一个幸运的日子，我们希望这一天的其余时间会保持这种状态。同样，我们可以认为我们已经发生了足够多的事故，现在确实需要做一些有趣的事情。从数学上讲，事情并非如此。如果您投掷普通硬币，那么您投掷正面或硬币的机会就完全相同。你已经扔了多少遍都没关系；下次投掷时，它仍然以相同的方式工作。抛硬币与其他抛硬币“无关”，不受抛硬币的影响。
   • 相信当您投掷硬币（或任何其他机会游戏）时，您可能是幸运的还是不幸的， 或者 您所有的厄运现在已经结束，而运气就在您这一边，这一事实也称为赌徒作弊（或赌徒的谬误）。这与人们倾向于在自己的身边，或者感到“幸运的连胜”，或者感到“好运即将来临”时做出危险或愚蠢的决定的倾向有关。
3. 了解大数定律。 您可能会认为期望值并不是真正有用的，因为它很少会告诉您情况的实际结果是什么。如果计算得出轮盘游戏的期望值为-€1，并且您玩了3次游戏，则通常最终会得到-€10，或+€60，或其他一些结果。 “大数法则”有助于解释为什么期望值比您想象的更有用：您玩的越多，平均结果就越接近期望值。当您查看大量事件时，最终结果很有可能接近预期值。

尖端

• 对于可能出现多个结果的情况，您可以在计算机中创建电子表格，以使用结果及其概率来计算期望值。
• 上面的€计算也可以使用其他货币。

生活必需品

• 铅笔
• 纸
• 计算器