内容

• 脚步
• 方法 1 of 5：查找多面体中的顶点数
• 方法 2 of 5：查找线性不等式系统域的顶点
• 方法 3 of 5：通过对称轴找到抛物线的顶点
• 方法 4 of 5：使用完整正方形的补集找到抛物线的顶点
• 方法 5 of 5：使用简单公式求抛物线的顶点
• 你需要什么

在数学中，有许多问题需要您找到顶部。例如，多面体的一个顶点、不等式系统域的一个或多个顶点、抛物线或二次方程的一个顶点。本文将向您展示如何在不同的问题中找到顶部。

脚步

方法 1 of 5：查找多面体中的顶点数

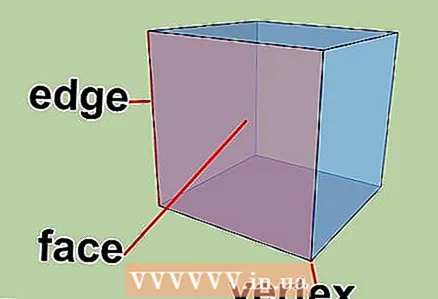1. 1 欧拉定理。 该定理指出，在任何多面体中，它的顶点数加上它的面数减去它的边数总是两个。
   • 描述欧拉定理的公式：F + V - E = 2
     • F是面数。
     • V 是顶点数。
     • E 为肋条数。
2. 2 重写公式以查找顶点数。 给定多面体的面数和边数，您可以使用欧拉公式快速找到顶点数。
   • V = 2 - F + E
3. 3 将你给出的值代入这个公式。 这为您提供了多面体中的顶点数。
   • 示例：求具有 6 个面和 12 条边的多面体的顶点数。
     • V = 2 - F + E
     • V = 2 - 6 + 12
     • V = -4 + 12
     • V = 8

方法 2 of 5：查找线性不等式系统域的顶点

1. 1 绘制线性不等式系统的解（面积）。 在某些情况下，您可以在图形上看到线性不等式系统区域的部分或全部顶点。否则，您必须以代数方式找到顶点。
   • 使用图形计算器时，您可以查看整个图形并找到顶点的坐标。
2. 2 将不等式转换为方程。 为了解决不等式系统（即找到“x”和“y”），您需要放置一个“等号”而不是不等号。
   • 示例：给定一个不等式系统：
     • y x
     • y> - x + 4
   • 将不等式转化为方程：
     • y = x
     • y = - x + 4
3. 3 现在在一个方程中表达任何变量并将其代入另一个方程。 在我们的示例中，将第一个方程中的 y 值插入到第二个方程中。
   • 例子：
     • y = x
     • y = - x + 4
   • 将 y = x 代入 y = - x + 4：
     • x = - x + 4
4. 4 找到其中一个变量。 现在你有一个只有一个变量 x 的方程，它很容易找到。
   • 示例：x = - x + 4
     • x + x = 4
     • 2x = 4
     • 2x / 2 = 4/2
     • x = 2
5. 5 找到另一个变量。 在任何等式中替换找到的值“x”并找到值“y”。
   • 示例：y = x
     • y = 2
6. 6 找到顶部。 顶点的坐标等于找到的值“x”和“y”。
   • 示例：给定不等式系统区域的顶点是点 O(2,2)。

方法 3 of 5：通过对称轴找到抛物线的顶点

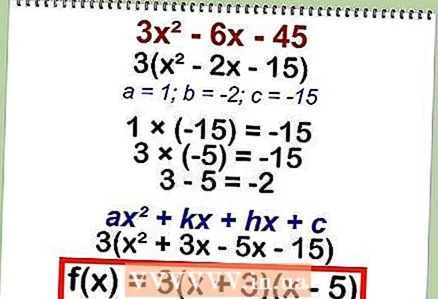1. 1 分解方程。 有几种方法可以分解二次方程。作为展开的结果，你得到两个二项式，当它们相乘时，将导致原始方程。
   • 例子：给定一个二次方程
     • 3x2 - 6x - 45
     • 首先，将公因数括起来：3 (x2 - 2x - 15)
     • 将系数“a”和“c”相乘：1 * (-15) = -15。
     • 找出两个数，它们的乘积为-15，它们的和等于系数“b”(b = -2)： 3 * (-5) = -15; 3 - 5 = -2。
     • 将找到的值代入方程 ax2 + kx + hx + c: 3 (x2 + 3x - 5x - 15)。
     • 展开原方程：f (x) = 3 * (x + 3) * (x - 5)
2. 2 找到函数图（在本例中为抛物线）与横坐标相交的点 (s)。 该图在 f (x) = 0 处与 X 轴交叉。
   • 示例：3 * (x + 3) * (x - 5) = 0
     • x +3 = 0
     • x - 5 = 0
     • x = -3; x = 5
     • 因此，方程的根（或与 X 轴的交点）：A (-3, 0) 和 B (5, 0)
3. 3 求对称轴。 函数的对称轴通过位于两个根之间的中间点。在这种情况下，顶点位于对称轴上。
   • 例子：x = 1;该值位于 -3 和 +5 之间。
4. 4 将 x 值代入原始方程并找到 y 值。 这些“x”和“y”值就是抛物线的顶点坐标。
   • 示例：y = 3x2 - 6x - 45 = 3 (1) 2 - 6 (1) - 45 = -48
5. 5 写下你的答案。
   • 例子：这个二次方程的顶点是点O(1, -48)

方法 4 of 5：使用完整正方形的补集找到抛物线的顶点

1. 1 将原方程改写为： y = a (x - h) ^ 2 + k，而顶点位于坐标为 (h, k) 的点上。为此，您需要将原始二次方程补充为一个完整的平方。
   • 示例：给定二次函数 y = - x ^ 2 - 8x - 15。
2. 2 考虑前两个术语。 分解第一项的系数（忽略截距）。
   • 示例：-1 (x ^ 2 + 8x) - 15。
3. 3 将自由项 (-15) 展开为两个数字，以便其中一个将括号中的表达式完成为一个完整的正方形。 其中一个数字必须等于第二项系数的一半的平方（来自括号中的表达式）。
   • 示例：8/2 = 4； 4 * 4 = 16;所以
     • -1 (x ^ 2 + 8x + 16)
     • -15 = -16 + 1
     • y = -1 (x ^ 2 + 8x + 16) + 1
4. 4 简化方程。 由于括号中的表达式是一个完整的正方形，您可以将这个等式重写为以下形式（如有必要，在括号外进行加法​​或减法运算）：
   • 示例：y = -1 (x + 4) ^ 2 + 1
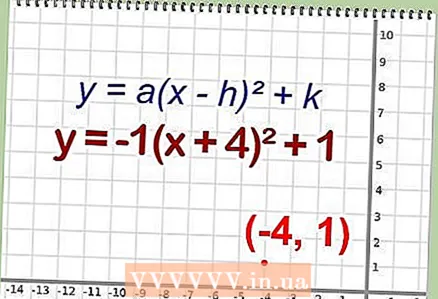5. 5 找到顶点的坐标。 回想一下形式为 y = a (x - h) ^ 2 + k 的函数的顶点坐标是 (h, k)。
   • k = 1
   • h = -4
   • 因此，原始函数的顶点是点 O(-4,1)。

方法 5 of 5：使用简单公式求抛物线的顶点

1. 1 使用以下公式找到“x”坐标： x = -b / 2a（对于形式为 y = ax ^ 2 + bx + c 的函数）。将“a”和“b”值代入公式，求出“x”坐标。
   • 示例：给定一个二次函数 y = - x ^ 2 - 8x - 15。
   • x = -b / 2a = - (- 8) / (2 * (- 1)) = 8 / (- 2) = -4
   • x = -4
2. 2 将您找到的 x 值代入原始方程。 因此，您会找到“y”。这些“x”和“y”值就是抛物线的顶点坐标。
   • 示例：y = - x ^ 2 - 8x - 15 = - (- 4) ^ 2 - 8 (-4) - 15 = - (16) - (- 32) - 15 = -16 + 32 - 15 = 1
     • y = 1
3. 3 写下你的答案。
   • 例子：原函数的顶点是点O(-4,1)。

你需要什么

• 计算器
• 铅笔
• 纸